Friday, June 21, 2013

ARMA模型

This post is from here.


ARMA模型（Auto-Regressive and Moving Average Model）

ARMA模型概述

　　ARMA 模型（Auto-Regressive and Moving Average Model）是研究时间序列的重要方法，由自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。在市场研究中常用于长期追踪资料的研究，如：Panel研究中，用于消费行为模式变迁研究；在零售研究中，用于具有季节变动特征的销售量、市场规模的预测等。
[编辑]

ARMA模型三种基本形式[1]

　　1.自回归模型（AR：Auto-regressive）；
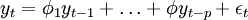
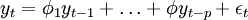
　　自回归模型AR(p)：如果时间序列yt满足y_t=\phi_1 y_{t-1}+\ldots+\phi y_{t-p}+\epsilon_t
　　其中εt是独立同分布的随机变量序列，且满足：
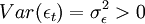
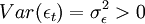
　　E(εt) = 0　　Var(\epsilon_t)=\sigma^2_\epsilon>0
　　则称时间序列为yt服从p阶的自回归模型。或者记为φ(B)yt = εt。
　　自回归模型的平稳条件：
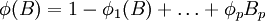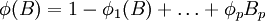　　滞后算子多项式\phi (B)=1-\phi_1(B)+\ldots+\phi_p B_p的根均在单位圆外，即φ(B) = 0的根大于1。
　　2.移动平均模型（MA：Moving-Average）
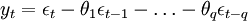
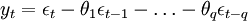
　　移动平均模型MA(q):如果时间序列yt满足y_t=\epsilon_t-\theta_1\epsilon_{t-1}-\ldots-\theta_q\epsilon_{t-q}
　　则称时间序列为yt服从q阶移动平均模型；
　　移动平均模型平稳条件：任何条件下都平稳。
　　3.混合模型（ARMA：Auto-regressive Moving-Average）
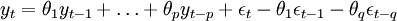
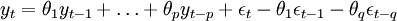
　　ARMA(p,q)模型：如果时间序列yt满足：y_t=\theta_1y_{t-1}+\ldots+\theta_p y_{t-p}+\epsilon_t-\theta_1\epsilon_{t-1}-\theta_q\epsilon_{t-q}
　　则称时间序列为yt服从(p,q)阶自回归滑动平均混合模型。或者记为φ(B)yt = θ(B)εt
　　特殊情况：q=0，模型即为AR(p)，p=0，模型即为MA(q)，
[编辑]

ARMA模型的基本原理

　　将预测指标随时间推移而形成的数据序列看作是一个随机序列，这组随机变量所具有的依存关系体现着原始数据在时间上的延续性。一方面，影响因素的影响，另一方面，又有自身变动规律，假定影响因素为x1，x2，…，xk，由回归分析，
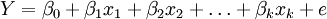
　　Y=\beta_0+\beta_1 x_1+\beta_2 x_2+\ldots+\beta_k x_k+e
　　其中Y是预测对象的观测值， e为误差。作为预测对象Yt受到自身变化的影响，其规律可由下式体现，
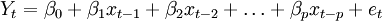
　　Y_t=\beta_0+\beta_1 x_{t-1}+\beta_2 x_{t-2}+\ldots+\beta_p x_{t-p}+e_t
　　误差项在不同时期具有依存关系，由下式表示，
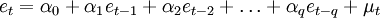
　　e_t=\alpha_0+\alpha_1 e_{t-1}+\alpha_2 e_{t-2}+\ldots+\alpha_q e_{t-q}+\mu_t
　　由此，获得ARMA模型表达式：
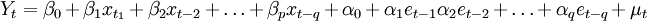
　　Y_t=\beta_0+\beta_1 x_{t_1}+\beta_2 x_{t-2}+\ldots+\beta_p x_{t-q}+\alpha_0+\alpha_1 e_{t-1}\alpha_2 e_{t-2}+\ldots+\alpha_q e_{t-q}+\mu_t
[编辑]

参考文献

  1. ↑ 徐国祥,马俊玲.《统计预测和决策》学习指导与习题[M].上海财经大学出版社.ISBN:7-81098-492-6.2005

Posted by at
Labels:

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)