5.1 单因素方差分析
5.1.1 方差分析的基本概念
在实际问题中,人们常常需要在不同的条件下对所研究的对象进行对比试验,从而得到若干组数据(样本)。方差分析就是一种分析、处理多组实验数据间均值差异的显著性的统计方法。其主要任务是,通过对数据的分析处理,搞清楚各实验条件对实验结果的影响,以便更有效地指导实践,提高经济效益或者科研水平。
在统计中,人们称受控制的条件为因素,因素所处的状态称为水平。
如果只让一个因素变动,取该因素的多个不同水平进行试验,而其他因素保持不变,称该试验为单因素试验。例如小麦种植产量,只考虑"品种"这一因素,研究4个不同品种产量的差异,其它诸如施肥方案、灌溉方案等因素保持一致,就是一个4水平单因素试验。
如果同时考虑两个因素,例如4个小麦品种在3种不同施肥方案下的产量,就是一个双因素试验。
对于 组实验数据,我们假定都来自正态总体,并且具有相同的方差(称为方差齐性),要检验这相互独立的
组实验数据,我们假定都来自正态总体,并且具有相同的方差(称为方差齐性),要检验这相互独立的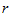 个正态总体
个正态总体
 组实验数据,我们假定都来自正态总体,并且具有相同的方差(称为方差齐性),要检验这相互独立的
组实验数据,我们假定都来自正态总体,并且具有相同的方差(称为方差齐性),要检验这相互独立的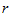 个正态总体
个正态总体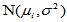
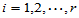
均值间有无差异,即:
H0: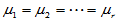 ; H1:诸
; H1:诸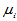 不全相同
不全相同
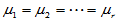 ; H1:诸
; H1:诸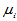 不全相同
不全相同
前面我们讲过两正态总体均值的假设检验,有T检验的方法。自然有一个想法,对于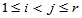 ,分别检验
,分别检验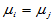 是否成立,若所有搭配均不拒绝,则接受H0,只要有一种搭配拒绝原假设认为
是否成立,若所有搭配均不拒绝,则接受H0,只要有一种搭配拒绝原假设认为 ,那就拒绝H0,看起来也不算麻烦。不妨称上述想法为"两两T检验法"。
,那就拒绝H0,看起来也不算麻烦。不妨称上述想法为"两两T检验法"。
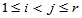 ,分别检验
,分别检验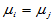 是否成立,若所有搭配均不拒绝,则接受H0,只要有一种搭配拒绝原假设认为
是否成立,若所有搭配均不拒绝,则接受H0,只要有一种搭配拒绝原假设认为 ,那就拒绝H0,看起来也不算麻烦。不妨称上述想法为"两两T检验法"。
,那就拒绝H0,看起来也不算麻烦。不妨称上述想法为"两两T检验法"。
回忆前面内容,设 为来自正态总体
为来自正态总体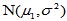 的简单随机样本,
的简单随机样本,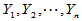 为来自正态总体
为来自正态总体 的简单随机样本,且两样本独立。为比较两个总体的期望,提出如下原假设:
的简单随机样本,且两样本独立。为比较两个总体的期望,提出如下原假设:
 为来自正态总体
为来自正态总体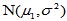 的简单随机样本,
的简单随机样本,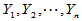 为来自正态总体
为来自正态总体 的简单随机样本,且两样本独立。为比较两个总体的期望,提出如下原假设:
的简单随机样本,且两样本独立。为比较两个总体的期望,提出如下原假设:
H0: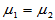
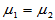
当H0成立时,检验统计量

我们给出函数t2test.m,解决上述计算问题。
function T=t2test(x,y)
m=length(x);
n=length(y);
vx=var(x);
vy=var(y);
a=(mean(x)-mean(y));
b=m+n-2;
c=(m-1)*vx+(n-1)*vy;
d=sqrt(m*n/(m+n));
T=a*d*sqrt(b/c);
以下给出m=10,n=10,且两总体皆服从标准正态分布的情形下,万次模拟的拒绝频率。以下命令文件保存为PnT2.m
N=10000;
m=10; n=10;
alpha=0.05;
t0=tinv(1-alpha/2,m+n-2);
P=0;
for k=1:N
x=randn(1,10); y=randn(1,10);
T=t2test(x,y);
if abs(T)>t0
P=P+1;
end
end
P=P/N
执行上述程序,发现每次频率都在0.05附近,说明上述两个正态总体均值的T检验的确是水平为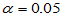 的检验。
的检验。
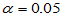 的检验。
的检验。
我们设想有8组数据,客观上都是来自标准正态分布,没有差异,每组样本容量都是10。现在用前述"两两T检验法"进行检验,下述程序计算出了万次模拟中拒绝的频率。
N=10000;
n=10; r=8;
alpha=0.05;
t0=tinv(1-alpha/2,n+n-2);
P=0;
for k=1:N
x=randn(8,10);
E=mean(x,2);
[EE,I]=sort(E);
X=x(I,:);
T=t2test(X(1,:),X(8,:));
if abs(T)>t0
P=P+1;
end
end
P=P/N
上述程序模拟发现,拒绝频率大约在0.45左右,严重偏离0.05,说明依照"两两T检验"犯第一类错误的概率严重增大,判定结果很不可靠。
对于8组数据,两两比较共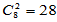 种组合,若每种组合接受原假设的概率为0.95,则28种组合都接受原假设的概率大致估计为
种组合,若每种组合接受原假设的概率为0.95,则28种组合都接受原假设的概率大致估计为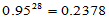 ,拒绝概率大致估计为0.76。由于相关性,拒绝概率没有达到0.76,但0.45也相当大了。
,拒绝概率大致估计为0.76。由于相关性,拒绝概率没有达到0.76,但0.45也相当大了。
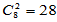 种组合,若每种组合接受原假设的概率为0.95,则28种组合都接受原假设的概率大致估计为
种组合,若每种组合接受原假设的概率为0.95,则28种组合都接受原假设的概率大致估计为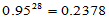 ,拒绝概率大致估计为0.76。由于相关性,拒绝概率没有达到0.76,但0.45也相当大了。
,拒绝概率大致估计为0.76。由于相关性,拒绝概率没有达到0.76,但0.45也相当大了。
为了避免上述问题的出现,1923年,波兰数学家R.A.Fisher提出了方差分析(Analysis of Variance简称ANOVA) 法,可以同时判定多组数据均值间差异的显著性检验问题。其检验统计量在H0成立时服从F分布,这里F分布就是以Fisher姓氏的第一个字母命名的。
5.1.2 单因素方差分析的计算
设有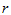 组数据,表示因素A的
组数据,表示因素A的 个水平,每组有
个水平,每组有 个观测值。我们已知实际结果具有以下结构:
个观测值。我们已知实际结果具有以下结构:
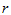 组数据,表示因素A的
组数据,表示因素A的 个水平,每组有
个水平,每组有 个观测值。我们已知实际结果具有以下结构:
个观测值。我们已知实际结果具有以下结构: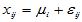 (
(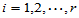 ;
;  )
) 表示水平Ai下的理论均值,
表示水平Ai下的理论均值, 为实验误差,诸
为实验误差,诸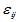 相互独立且服从正态分布
相互独立且服从正态分布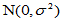 。
。
为了看出因素A个水平影响的大小,将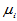 进行分解,令
进行分解,令
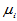 进行分解,令
进行分解,令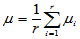 ,
, 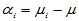
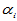 表示水平Ai对试验结果的影响,称为Ai的水平效应。显然
表示水平Ai对试验结果的影响,称为Ai的水平效应。显然
这时数据有如下结构:
 (
(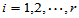 ;
;  ) (5-1)
) (5-1)
于是,我们需要进行的假设检验为:
H0: ; H1:诸
; H1:诸 不全为零 (5-2)
不全为零 (5-2)
 ; H1:诸
; H1:诸 不全为零 (5-2)
不全为零 (5-2)
记
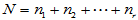
 ,(
,( ) ,
) , 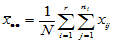
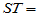
 (5-3)
(5-3)
称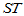 为总离差平方和,它反映了样本观测值之间的总的变异程度。以下我们将
为总离差平方和,它反映了样本观测值之间的总的变异程度。以下我们将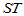 分解为两部分,以便区别水平效应与随机误差的影响。
分解为两部分,以便区别水平效应与随机误差的影响。
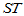 为总离差平方和,它反映了样本观测值之间的总的变异程度。以下我们将
为总离差平方和,它反映了样本观测值之间的总的变异程度。以下我们将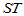 分解为两部分,以便区别水平效应与随机误差的影响。
分解为两部分,以便区别水平效应与随机误差的影响。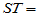
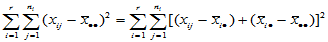
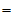
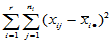
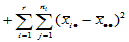

其中
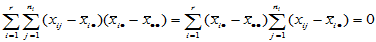
记
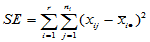 ,
,  (5-4)
(5-4)
称 为组内平方和,它反映了每组的组内随机误差。称
为组内平方和,它反映了每组的组内随机误差。称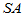 为组间平方和,反应的是组与组之间的差异。上述推导说明,总离差平方可以分解为
为组间平方和,反应的是组与组之间的差异。上述推导说明,总离差平方可以分解为
 为组内平方和,它反映了每组的组内随机误差。称
为组内平方和,它反映了每组的组内随机误差。称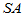 为组间平方和,反应的是组与组之间的差异。上述推导说明,总离差平方可以分解为
为组间平方和,反应的是组与组之间的差异。上述推导说明,总离差平方可以分解为 (5-5)
(5-5)
一个自然的想法是:如果在总离差平方和中, 所占比例很大,则拒绝原假设,认为客观上存在水平效应。
所占比例很大,则拒绝原假设,认为客观上存在水平效应。
 所占比例很大,则拒绝原假设,认为客观上存在水平效应。
所占比例很大,则拒绝原假设,认为客观上存在水平效应。
在H0成立时容易计算
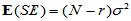 ;
; 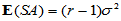 (5-6)
(5-6)
因此,当H0成立时,有
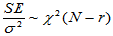 ,
, 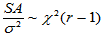 (5-7)
(5-7)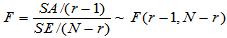 (5-8)
(5-8)
对于自由度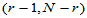 ,求临界值
,求临界值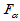 ,当
,当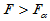 时拒绝H0即可。
时拒绝H0即可。
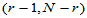 ,求临界值
,求临界值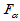 ,当
,当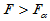 时拒绝H0即可。
时拒绝H0即可。
表5-1 单因素方差分析表
方差来源
|
平方和
|
自由度
|
均方
|
F值
|
临界值
|
显著性
|
组间
|
SA
| 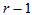 | 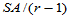 | 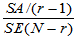 | 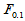 | |
误差
|
SE
| 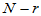 | 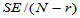 | 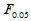 | ||
总和
|
ST
| 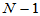 | 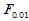 |
实际计算时常采用方差分析表,如表5-1所示。当 时,称为不显著,即认为各组均值之间没有显著差异,在显著性一栏不做任何标记。当
时,称为不显著,即认为各组均值之间没有显著差异,在显著性一栏不做任何标记。当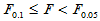 时,称为较显著,即认为各组均值之间有较显著差异,在显著性一栏用(*)标记。当
时,称为较显著,即认为各组均值之间有较显著差异,在显著性一栏用(*)标记。当 时,称为显著,即认为各组均值之间有显著差异,在显著性一栏用*标记。当
时,称为显著,即认为各组均值之间有显著差异,在显著性一栏用*标记。当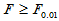 时,称为极显著,即认为各组均值之间有极显著差异,在显著性一栏用**标记。
时,称为极显著,即认为各组均值之间有极显著差异,在显著性一栏用**标记。
 时,称为不显著,即认为各组均值之间没有显著差异,在显著性一栏不做任何标记。当
时,称为不显著,即认为各组均值之间没有显著差异,在显著性一栏不做任何标记。当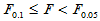 时,称为较显著,即认为各组均值之间有较显著差异,在显著性一栏用(*)标记。当
时,称为较显著,即认为各组均值之间有较显著差异,在显著性一栏用(*)标记。当 时,称为显著,即认为各组均值之间有显著差异,在显著性一栏用*标记。当
时,称为显著,即认为各组均值之间有显著差异,在显著性一栏用*标记。当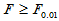 时,称为极显著,即认为各组均值之间有极显著差异,在显著性一栏用**标记。
时,称为极显著,即认为各组均值之间有极显著差异,在显著性一栏用**标记。
上述传统的方差计算表,在计算机普及后稍有变动,表中最后两列可以变动为直接计算H0成立时F分布大于此F值的概率,是否显著一看自明。
例5.1 为了研究三种不同伤寒杆菌对于小白鼠存活天数的影响,分三组实验,实验数据如下:
A1: 2, 4, 3, 2, 4, 7, 7, 2, 5, 4
A2: 5, 6, 8, 5, 10,7, 12,6, 6
A3: 7, 11,6, 6, 7, 9, 5, 10,6, 3,10
试检验不同伤寒杆菌对于小白鼠存活天数有无显著影响?
解 原假设H0没有显著差异。以下利用Matlab计算,并将计算结果汇总到表5-2中。
x1=[2, 4, 3, 2, 4, 7, 7, 2, 5, 4];
x2=[5, 6, 8, 5, 10,7, 12,6, 6];
x3=[7, 11,6, 6, 7, 9, 5, 10,6, 3,10];
n1=length(x1);
n2=length(x2);
n3=length(x3);
X1=sum(x1), mx1=mean(x1),
X2=sum(x2), mx2=mean(x2),
X3=sum(x3), mx3=mean(x3),
n=n1+n2+n3, X=X1+X2+X3, mx=X/n,
SE=(x1-mx1)*(x1-mx1)'+(x2-mx2)*(x2-mx2)'+(x3-mx3)*(x3-mx3)',
SA=n1*(mx1-mx)^2+n2*(mx2-mx)^2+n3*(mx3-mx)^2,
F=(SA/2)/(SE/27),
finv(0.9,2,27),
finv(0.95,2,27),
finv(0.99,2,27),
p=1-fcdf(F,2,27),
表5-2 不同伤寒杆菌对小白鼠存活天数影响的方差分析表
方差来源
|
平方和
|
自由度
|
均方
|
F值
|
临界值
|
显著性
|
组间
|
70.4293
|
2
|
35.2146
|
6.9030
|
2.5106
|
**
|
误差
|
137.7374
|
27
|
5.1014
|
3.3541
| ||
总和
|
208.1667
|
29
|
5.4881
|
可以认为不同伤寒杆菌对小白鼠存活天数有极显著影响。
上述最后一行命令执行的结果为p=0.0038,实际判定时,此值更能说明显著性程度。
当各组样本容量相等时,Matlab自带了单因素方差分析函数anova1,并且自动返回类似的方差分析表,调用格式为anova1(x),这里x为矩阵,按列分组,第一列为第一组数据,要求每组数据相同。
例5.2 某班学生共分别住在四个宿舍,某次英语水平考试成绩如下:
表5-3 各宿舍学生英语成绩表
宿舍一
|
86
|
74
|
78
|
76
|
73
|
82
|
宿舍二
|
59
|
76
|
63
|
66
|
75
|
65
|
宿舍三
|
79
|
71
|
82
|
66
|
87
|
96
|
宿舍四
|
86
|
91
|
95
|
77
|
88
|
85
|
问不同宿舍学生英语水平有无显著差异?
解 利用复制粘贴的办法输入矩阵x,由于anova1要求按列分组,故使用x=x'命令,然后再执行命令
p=anova1(x),
返回值为p =0.002,故差异极显著。Matlab同时返回了两个图形。

图5-1 Matlab中anova1返回的方差分析表

图5-2 Matlab中anova1返回的各组数据图
图5-2中各线含义依次为:最小值、1/4分位数、中位数、3/4分位数、最大值。
5.1.3 单因素方差分析的多重比较
经过方差分析之后,如果拒绝原假设,认为各组之间的均值有显著差异,那么,这个判断是对整体而言的,并不是说每两个不同的组之间均值都存在显著差异。那么,如何确定哪两个组之间有显著差异、无显著差异呢?这就要对每种搭配做一对一的比较,即多重比较。Matlab提供了multcompare函数用于进行多重比较,为了使用这个函数,在用anova1做方差分析的时候要使用如下的三个输出的调用格式
[P,ANOVATAB,STATS] = anova1(x)
在例5.2的数据输入之后,假定x已经经过转置使得每组数据按列排列,执行上述命令后,则除了返回上述两个图形外,还返回
P =
0.0020
ANOVATAB =
'Source' 'SS' 'df' 'MS' 'F' 'Prob>F'
'Columns' [1.1963e+003] [ 3] [398.7778] [7.0768] [0.0020]
'Error' [1.1270e+003] [20] [ 56.3500] [] []
'Total' [2.3233e+003] [23] [] [] []
STATS =
gnames: [4x1 char]
n: [6 6 6 6]
source: 'anova1'
means: [78.1667 67.3333 80.1667 87]
df: 20
s: 7.5067
其中最后一个输出结果STATS用于多重比较函数调用。继续执行命令
COMPARISON = multcompare(STATS,'alpha',0.1)
得到输出结果
COMPARISON =
1.0000 2.0000 0.2251 10.8333 21.4415
1.0000 3.0000 -12.6082 -2.0000 8.6082
1.0000 4.0000 -19.4415 -8.8333 1.7749
2.0000 3.0000 -23.4415 -12.8333 -2.2251
2.0000 4.0000 -30.2749 -19.6667 -9.0585
3.0000 4.0000 -17.4415 -6.8333 3.7749
上述结果中,逐行显示一对一比较的结果。第一列与第二列是参与比较的组号,第三列与第五列是均值差的置信区间,置信水平由输入变量alpha=0.1确定。第四列为两组样本均值的差。若第三列置信下限与第五列置信上限正负符号相同,则差异显著。由于alpha=0.1,我们可以发现第1,2组差异较显著,第2,3组差异较显著,第2,4组差异较显著,其它对比差异不显著。
再修改上述输入变量alpha的值,重新计算
COMPARISON = multcompare(STATS,'alpha',0.05)
输出结果为
COMPARISON =
1.0000 2.0000 -1.2972 10.8333 22.9639
1.0000 3.0000 -14.1305 -2.0000 10.1305
1.0000 4.0000 -20.9639 -8.8333 3.2972
2.0000 3.0000 -24.9639 -12.8333 -0.7028
2.0000 4.0000 -31.7972 -19.6667 -7.5361
3.0000 4.0000 -18.9639 -6.8333 5.2972
只有第2,3组,第2,4组有显著差异。继续执行
COMPARISON = multcompare(STATS,'alpha',0.01)
输出结果为
COMPARISON =
1.0000 2.0000 -4.5448 10.8333 26.2115
1.0000 3.0000 -17.3781 -2.0000 13.3781
1.0000 4.0000 -24.2115 -8.8333 6.5448
2.0000 3.0000 -28.2115 -12.8333 2.5448
2.0000 4.0000 -35.0448 -19.6667 -4.2885
3.0000 4.0000 -22.2115 -6.8333 8.5448
发现只有第2,4组有极显著的差异。
5.2 双因素方差分析
5.2.1 有重复实验的双因素方差分析
如果实验同时受到两个因素的共同影响,因素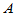 有
有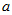 个水平,因素
个水平,因素 有
有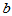 个水平,一共有
个水平,一共有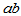 种搭配方案,每种搭配有做
种搭配方案,每种搭配有做 个实验数据,实验数据表依照表5-4所示排列。
个实验数据,实验数据表依照表5-4所示排列。
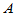 有
有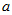 个水平,因素
个水平,因素 有
有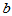 个水平,一共有
个水平,一共有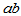 种搭配方案,每种搭配有做
种搭配方案,每种搭配有做 个实验数据,实验数据表依照表5-4所示排列。
个实验数据,实验数据表依照表5-4所示排列。
首先引进记号
在 的三个下标中,若有的下标为点,则表示对该下标求和,例如
的三个下标中,若有的下标为点,则表示对该下标求和,例如
 的三个下标中,若有的下标为点,则表示对该下标求和,例如
的三个下标中,若有的下标为点,则表示对该下标求和,例如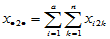 ,
,  ,
, 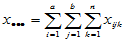
相应的平均值记为
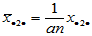 ,
,  ,
, 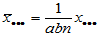
依此类推。
将上述诸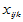 看成是随机变量,并且假设满足以下线性模型
看成是随机变量,并且假设满足以下线性模型
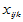 看成是随机变量,并且假设满足以下线性模型
看成是随机变量,并且假设满足以下线性模型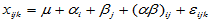 ,
, 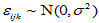 (5-9)
(5-9) ,
, ,
,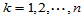
表5-4 双因素有重复试验数据表
因素
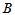 | |||||
 | 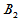 | 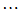 |  | ||
因
素
 |  | 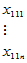 |  |  | 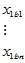 |
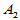 | 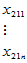 | 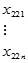 |  |  | |
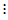 | 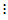 |  |  | ||
 | 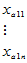 |  |  | ||
其中 是各种搭配下的总平均数的理论值,
是各种搭配下的总平均数的理论值, 是因素
是因素 的第
的第 个水平的效应,
个水平的效应,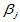 是因素
是因素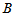 的第
的第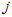 个水平的效应,
个水平的效应,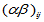 是
是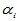 与
与 的交互作用,即搭配效应。
的交互作用,即搭配效应。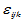 是相互独立的正态随机变量,均值为零,方差为
是相互独立的正态随机变量,均值为零,方差为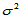 ,并且诸
,并且诸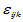 相互独立。满足
相互独立。满足
 是各种搭配下的总平均数的理论值,
是各种搭配下的总平均数的理论值, 是因素
是因素 的第
的第 个水平的效应,
个水平的效应,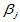 是因素
是因素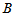 的第
的第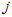 个水平的效应,
个水平的效应,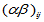 是
是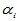 与
与 的交互作用,即搭配效应。
的交互作用,即搭配效应。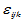 是相互独立的正态随机变量,均值为零,方差为
是相互独立的正态随机变量,均值为零,方差为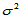 ,并且诸
,并且诸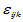 相互独立。满足
相互独立。满足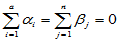 ,
, (5-10)
(5-10)
对于上述有重复试验的双因素实验,方差分析检验如下三个假设:
H01: (5-11)
(5-11)
 (5-11)
(5-11)
H02: (5-12)
(5-12)
 (5-12)
(5-12)
H03: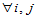 ,
,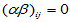 (5-13)
(5-13)
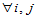 ,
,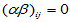 (5-13)
(5-13)
类似单因素方差分析,记总离差平方和为
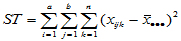 (5-14)
(5-14)
则有如下分解式
 自由度为
自由度为 (5-15)
(5-15)
其中
 , 自由度为
, 自由度为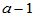 (5-16)
(5-16) , 自由度为
, 自由度为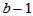 (5-17)
(5-17)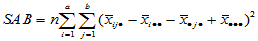 , 自由度为
, 自由度为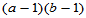 (5-18)
(5-18)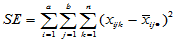 , 自由度为
, 自由度为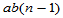 (5-19)
(5-19)
由此可得检验统计量,当H01成立时,
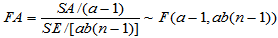 (5-20)
(5-20)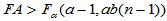 时,拒绝H01,认为因素
时,拒绝H01,认为因素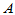 作用显著。
作用显著。
当H02成立时,
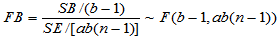 (5-21)
(5-21)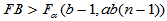 时,拒绝H02,认为因素
时,拒绝H02,认为因素 作用显著。
作用显著。
当H03成立时,
 (5-22)
(5-22) 时,拒绝H03,认为交互作用显著。
时,拒绝H03,认为交互作用显著。
方差计算可以类似地用方差计算表进行。
Matlab自带的函数anova2用于处理双因素方差分析,调用格式为
[P,TABLE,STATS] = anova2(x,n)
其中P返回概率值,TABLE返回方差计算表,STATS返回的信息用于多重比较。输入变量n表示每种搭配下样本容量,记号同前述公式。x为数据矩阵,为na行b列,格式与表5-4完全一致。
例5.3 杨树一年中生长高度受两种因素影响,A:施肥方案,B:深翻方案。对于4种施肥方案及3种深翻方案,共12种搭配,各实验3株,实验结果如表5-5所示。试问施肥方案、深翻方案、两者的交互作用对于苗高有无显著影响?
表5-5 杨树苗增高实验数据表
B1
|
B2
|
B3
| |
A1
|
52 43 39
|
41 47 53
|
49 38 42
|
A2
|
48 37 29
|
50 41 30
|
36 48 47
|
A3
|
34 42 38
|
36 39 44
|
37 40 32
|
A4
|
45 58 42
|
44 46 60
|
43 56 41
|
解 利用复制粘贴的办法对矩阵x赋值,注意到anova2的要求,重复数据按列排列,故对x进行转置,x=x'。转置之后x为9行4列矩阵,每列表示4种施肥方案的数据,行对应的是3种深翻方案。执行Matlab命令:
[P,TABLE,STATS] = anova2(x,3)
计算结果为:
P =
0.0259 0.7504 0.9540
TABLE =
'Source' 'SS' 'df' 'MS' 'F' 'Prob>F'
'Columns' [ 562.0833] [ 3] [187.3611] [3.6838] [0.0259]
'Rows' [ 29.5556] [ 2] [ 14.7778] [0.2906] [0.7504]
'Interaction' [ 76.6667] [ 6] [ 12.7778] [0.2512] [0.9540]
'Error' [1.2207e+003] [24] [ 50.8611] [] []
'Total' [1.8890e+003] [35] [] [] []
STATS =
source: 'anova2'
sigmasq: 50.8611
colmeans: [44.8889 40.6667 38 48.3333]
coln: 9
rowmeans: [42.2500 44.2500 42.4167]
rown: 12
inter: 1
pval: 0.9540
df: 24
同时返回图形,图形中显示了方差分析表。诸列(Columns)表示的是4种施肥方案,诸行(Rows)表示的是3种深翻方案,从上述方差分析表中可以看出,施肥方案有显著影响,深翻方案无显著影响,两因素间无交互作用。
COMPARISON = multcompare(STATS,'alpha',0.05)
结果显示
Note: Your model includes an interaction term. A test of main
effects can be difficult to interpret when the model includes
interactions.
COMPARISON =
1.0000 2.0000 -5.0520 4.2222 13.4964
1.0000 3.0000 -2.3853 6.8889 16.1631
1.0000 4.0000 -12.7187 -3.4444 5.8298
2.0000 3.0000 -6.6075 2.6667 11.9409
2.0000 4.0000 -16.9409 -7.6667 1.6075
3.0000 4.0000 -19.6075 -10.3333 -1.0591
多重比较的结果发现,第3,4种施肥方案差异显著。Matlab返回的注释说明,对于有交互项的情形,上述多重比较仅供参考。
5.2.2 无重复实验的双因素方差分析
要把交互作用与随机误差区别开,就必须对每种搭配进行重复试验。如果两个因素间确无交互作用,线性模型可以简化为:
 ,
,  (5-23)
(5-23)
此时检验H01与H02即可。
利用anova2仍可进行方差分析,其原理仍是平方和分解与 检验。不再一一罗列公式。
检验。不再一一罗列公式。
 检验。不再一一罗列公式。
检验。不再一一罗列公式。
例5.4 某养猪场进行猪增重试验,选择4个品种的猪和3种饲料,共12中搭配方案,每种饲养一头,三个月后增重数据如表5-6所示。试研究品种与饲料对于猪增重的影响。
解 复制粘贴输入数据矩阵x,执行
[P,TABLE,STATS] = anova2(x)
表5-6 猪增重数据表
饲料1
|
饲料2
|
饲料3
| |
品种1
|
51
|
53
|
52
|
品种2
|
56
|
57
|
58
|
品种3
|
45
|
49
|
47
|
品种4
|
42
|
44
|
43
|
计算结果为:
P =
0.0156 0.0000
TABLE =
'Source' 'SS' 'df' 'MS' 'F' 'Prob>F'
'Columns' [ 10.5000] [ 2] [ 5.2500] [ 9] [ 0.0156]
'Rows' [332.2500] [ 3] [110.7500] [189.8571] [2.4683e-006]
'Error' [ 3.5000] [ 6] [ 0.5833] [] []
'Total' [346.2500] [11] [] [] []
STATS =
source: 'anova2'
sigmasq: 0.5833
colmeans: [48.5000 50.7500 50]
coln: 4
rowmeans: [52 57 47 43]
rown: 3
inter: 0
pval: NaN
df: 6
可以看出,诸列(Columns)间差异显著,说明饲料作用显著;诸行(Rows)间差异极显著,说明在这4个猪的品种间,增重差异极显著。
对于无重复实验可以可靠地进行多重比较。继续计算:
COMPARISON = multcompare(STATS,'alpha',0.05, 'estimate','column')
结果为
COMPARISON =
1.0000 2.0000 -3.9071 -2.2500 -0.5929
1.0000 3.0000 -3.1571 -1.5000 0.1571
2.0000 3.0000 -0.9071 0.7500 2.4071
发现第1,2种饲料差异显著。
COMPARISON = multcompare(STATS,'alpha',0.05, 'estimate','row')
结果为
COMPARISON =
1.0000 2.0000 -7.1588 -5.0000 -2.8412
1.0000 3.0000 2.8412 5.0000 7.1588
1.0000 4.0000 6.8412 9.0000 11.1588
2.0000 3.0000 7.8412 10.0000 12.1588
2.0000 4.0000 11.8412 14.0000 16.1588
3.0000 4.0000 1.8412 4.0000 6.1588
4个猪的品种,每种搭配对比,增重差异都显著。
COMPARISON = multcompare(STATS,'alpha',0.01, 'estimate','row')
结果为
COMPARISON =
1.0000 2.0000 -8.1014 -5.0000 -1.8986
1.0000 3.0000 1.8986 5.0000 8.1014
1.0000 4.0000 5.8986 9.0000 12.1014
2.0000 3.0000 6.8986 10.0000 13.1014
2.0000 4.0000 10.8986 14.0000 17.1014
3.0000 4.0000 0.8986 4.0000 7.1014
4个猪的品种,每种搭配对比,增重差异都极显著。
No comments:
Post a Comment